- Una superficie de revolución cilíndrica es generada por la rotación de una línea recta, paralela al eje de rotación, alrededor del mismo; esta superficie determina un volumen denominado cilindro, que se denomina sólido de revolución; la distancia entre el eje y la recta se denomina radio.
- Una superficie de revolución cónica es generada por la rotación de una recta alrededor de un eje al cual interseca en un punto, llamado vértice o ápice, de forma que el ángulo bajo el que la generatriz corta al eje es constante; la superficie cónica delimita alvolumen denominado cono.
- Una superficie de revolución esférica está generada por la rotación de una semicircunferencia alrededor de su diámetro; ésta encierra al sólido de revolución llamado esfera.
- Una superficie de revolución toroidal está generada por la rotación de una circunferencia alrededor de un eje que no la interseca en ningún punto; esta superficie se denomina toro.
Área de una superficie de revolución
Si la curva está definida por las funciones  y
y 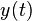 , perteneciendo
, perteneciendo  a un intervalo
a un intervalo ![[a,b]](http://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) y siendo el eje de revolución el eje coordenado
y siendo el eje de revolución el eje coordenado  , el área
, el área  estará dada, entonces, por la integral
estará dada, entonces, por la integral
 y
y 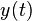 , perteneciendo
, perteneciendo  a un intervalo
a un intervalo ![[a,b]](http://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) y siendo el eje de revolución el eje coordenado
y siendo el eje de revolución el eje coordenado  , el área
, el área  estará dada, entonces, por la integral
estará dada, entonces, por la integral
siendo  siempre positiva. Esta ecuación es equivalente al Teorema del centroide de Pappus. Asimismo, la cantidad
siempre positiva. Esta ecuación es equivalente al Teorema del centroide de Pappus. Asimismo, la cantidad
 siempre positiva. Esta ecuación es equivalente al Teorema del centroide de Pappus. Asimismo, la cantidad
siempre positiva. Esta ecuación es equivalente al Teorema del centroide de Pappus. Asimismo, la cantidad
se deriva del teorema de Pitágoras y representa un segmento diferencial del arco de la curva, como en la ecuación de la longitud de arco. La cantidad  es el camino descrito por el centroide de dicho segmento girando alrededor del eje de revolución.
es el camino descrito por el centroide de dicho segmento girando alrededor del eje de revolución.
 es el camino descrito por el centroide de dicho segmento girando alrededor del eje de revolución.
es el camino descrito por el centroide de dicho segmento girando alrededor del eje de revolución.
Si la curva está definida por la función 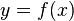 , la integral se transforma en
, la integral se transforma en
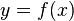 , la integral se transforma en
, la integral se transforma en
para una curva que gira alrededor del eje de las ordenadas.
Como ejemplo, la esfera, con un radio unitario, está generada por la curva  y
y  cuando
cuando  toma valores en el intervalo
toma valores en el intervalo ![[0,\pi]](http://upload.wikimedia.org/math/e/1/8/e1868564b62b4e2f1c063321df289469.png) . Su área, por tanto, será
. Su área, por tanto, será
 y
y  cuando
cuando  toma valores en el intervalo
toma valores en el intervalo ![[0,\pi]](http://upload.wikimedia.org/math/e/1/8/e1868564b62b4e2f1c063321df289469.png) . Su área, por tanto, será
. Su área, por tanto, seráGeometría diferencial de superficies de revolución
Una superficie de revolución puede ser parametrizada mediante una coordenada a lo largo de su generatriz u y una coordenada angular v de tal manera que:
Las curvas con u = constante, son círculos llamados paralelos, mientras que las líneas con v = constante, llamados meridianos son líneas geodésicas de longitud y curvatura mínimas. Además los coeficientes de la primera forma fundamental o tensor métrico de una superficie resultan ser:
Por lo que la métrica es diagonal. En cuanto a la segunda forma fundamental relacionada con la curvatura de la superficie también toma una forma particularmente simple:
![[II_{kl}(u,v)] =\begin{pmatrix} L(u,v) & M(u,v) \\ M(u,v) & N(u,v) \end{pmatrix} =
\begin{pmatrix} \frac{\rho_uh_{uu}-\rho_{uu}h_u}{\sqrt{E}} & 0 \\ 0 & \frac{\rho h_u}{\sqrt{E}} \end{pmatrix}](http://upload.wikimedia.org/math/6/2/5/625e741be04b966cc1535ad5628663c6.png)
Teorema del centroide de Pappus
Teorema del centroide de Pappus, también conocido como teorema de Guldin, teorema de Pappus-Guldin o teorema de Pappus, es el nombre de dos teoremas que relacionan superficies y volúmenes de sólidos de revolución con sus respectivos centroides.Los teoremas se les atribuyen a Pappus de Alejandría y a Paul Guldin.Primer Teorema
Sea una curva plana definida por la función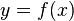 , en un intervalo cerrado
, en un intervalo cerrado ![[a, b]](http://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) donde es continua. Entonces, el área del sólido de revolución que se genera al girar la curva alrededor del eje de las
donde es continua. Entonces, el área del sólido de revolución que se genera al girar la curva alrededor del eje de las  es:
es: Por otra parte, la coordenada
Por otra parte, la coordenada del centroide de esta curva se calcula así:
del centroide de esta curva se calcula así: Ya que
Ya que es la longitud de la curva plana indicada en el denominador.Es fácil inferir que la ecuación () se transforma en:
es la longitud de la curva plana indicada en el denominador.Es fácil inferir que la ecuación () se transforma en: Con lo cual se completa la demostración.
Con lo cual se completa la demostración.Segundo Teorema
Sean dos funciones y
y  continuas y definidas en el intervalo
continuas y definidas en el intervalo ![[a, b]](http://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , tales que
, tales que  y que delimitan una región plana de área
y que delimitan una región plana de área  . El volumen
. El volumen 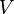 del sólido de revolución que se genera al hacer girar esta región alrededor del eje x se calcula mediante el método de los anillos, lo que da como resultado:
del sólido de revolución que se genera al hacer girar esta región alrededor del eje x se calcula mediante el método de los anillos, lo que da como resultado: Por otra parte, para calcular la coordenada
Por otra parte, para calcular la coordenada del centroide de una región plana delimitada por las curvas
del centroide de una región plana delimitada por las curvas  y
y  se emplea esta ecuación:
se emplea esta ecuación: Ya que
Ya que es el área comprendida por las dos curvas. Por tanto, la ecuación del volumen debe volver a ser escrita como:
es el área comprendida por las dos curvas. Por tanto, la ecuación del volumen debe volver a ser escrita como: lo que completa la demostración. Si el cálculo se refiere a la coordenada
lo que completa la demostración. Si el cálculo se refiere a la coordenada el cálculo es semejante, haciendo la salvedad de que, en este caso:
el cálculo es semejante, haciendo la salvedad de que, en este caso:![V= 2\pi \int_a^b x*[f(x) - g(x)] \,dx](http://upload.wikimedia.org/math/4/3/c/43ced25df2dcc5fda52c48386114becf.png) aunque el área se calcula como ya se indicó al principio.En caso de que se desee calcular el volumen del sólido de revolución alrededor de una recta que no tenga intersección con el área, de la forma
aunque el área se calcula como ya se indicó al principio.En caso de que se desee calcular el volumen del sólido de revolución alrededor de una recta que no tenga intersección con el área, de la forma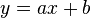 aún se puede emplear este teorema a condición de que se calcule la distancia entre el centroide y dicha recta.
aún se puede emplear este teorema a condición de que se calcule la distancia entre el centroide y dicha recta.






![[I_{kl}(u,v)] =\begin{pmatrix} E(u,v) & F(u,v) \\ F(u,v) & G(u,v) \end{pmatrix} =
\begin{pmatrix} \rho_u^2(u)+h_u^2(u) & 0 \\ 0 & \rho^2(u) \end{pmatrix}](http://upload.wikimedia.org/math/b/6/b/b6bd8715e42315a86441f5655491a8c4.png)
No hay comentarios:
Publicar un comentario